
UNIVERSITY OF TORONTO DEPARTMENT OF COMPUTER SCIENCE
One Cube
Yawen(Frank) Tian
April 8, 2014
1. BACKGROUND
Rubik’s Cube is a
1

UNIVERSITY OF TORONTO DEPARTMENT OF COMPUTER SCIENCE
One Cube
Yawen(Frank) Tian
April 8, 2014
1. BACKGROUND
Rubik’s Cube is a
1
1.1. MOTIVATION OF THE PROJECT
Originally the project was intended to create a digital version of Rubik’s Cube in a 3D imple- mentation within mobile device(Android, iOS) in the sense that the existing apps are not real 3D but more 2.5D. Given the situation that the idea for mobile Rubik’s Cube existed and there are implementations published already. Professor Karan Singh gave me a new idea of creating a
The skeleton of One Cube is exactly the same as a standard 3 by 3 Rubik’s Cube with one core difference in the rotation: In a standard Rubik’s Cube, the elementary movement is a 90± rotation in one of the faces. While the elementary move for One Cube is, bascally, a 30± rotations in one of the rows.
Notice from here that I am using the term ROW and 30± compare to F ACE and 90± for Rubik’s Cube. This represents the core mechanical difference between One Cube and Rubik’s Cube. The rotation for One Cube is like rotation of the continuous track in a tank. For a single rotation, each of the twelve faces within the row being rotated get moved one unit position towards the direction of this rotation. For a complete cycle you need to perform twelve basic rotation to the rotating row.
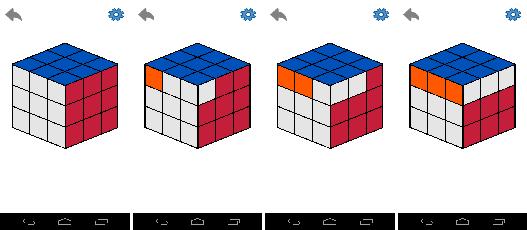
The figure below shows three basic rotation of One Cube to simulate a basic rotation of Rubik’s Cube
Notice that the small squares in One Cube is generally more independent than Rubik’s Cube, in the sense that Rubik’s Cube is a combination of 26 small pieces while One Cube is a combi- nation of 54 squares. This also leads to the total permutations of One Cube dramatically larger than Rubik’s Cube, which I will go over in the later section.
2

2. IMPLEMENTATION
The current version of the project is implemented for Android device. The part can be divided into two parts. The data structure and the
2.1. DATA STRUCTURE
Given the behaviour of One Cube, I am using linked list as the idea achieve the desire outcome. The component of the whole cube breaks into two main areas: The cube and the face.
// Cube.java
public class Cube {
public Face front1 = new Face(); public Face back1 = new Face(); public Face left1 = new Face(); public Face right1 = new Face(); public Face up1 = new Face(); public Face down1 = new Face();
public Face front2 = new Face(); public Face back2 = new Face(); public Face left2 = new Face(); public Face right2 = new Face(); public Face up2 = new Face(); public Face down2 = new Face();
//More Face declaration
...
//Methods
...
}
public class Face {
private String color; // The color that this face currently holds
// Adjacent faces private Face up; private Face down; private Face left; private Face right;
private String id; // Represent the absolute location of this face
// Methods
...
}
3

It is easy to see that there are 54 faces in total. Each face acts as node within the linked list. All of them are mutually connected with the four pointers up, down, left right. This kind of data structure enables me to perform the rotation from the code level in a very day and smooth way:
/**
* Perform a basic left rotation on the current face */
public void rotateLeft () {
String temp = this.getColor(); String originID = this.getID(); Face3 current = this;
do {
// Switch the colour on at a time current.setColor(current.getRight().getColor()); current = current.getRight();
} while(current.getID() != originID); current.getLeft().setColor(temp);
}
2.2. FRONT END IMPLEMENTATION
The front end implementation is achieved by Android and OpenGL. The most challenging but also the most interesting part is the implementation of the touch event. And this is also where I got most of my critiques from the professor. In order to create a better user experience. It is nice for the player to be able to rotate the cube continuously rather than a single move upon touch release.
Take the screen of a mobile device is
Boundary left1 = new Boundary(
new Point((double)60.0f/720*getWidth(), (500.0f - 3*d0)/1280*getHeight()), //upLeft
new Point((double)160.0f/720*getWidth(), (500.0f - 2*d0)/1280*getHeight()), //upRight
new Point((double)160.0f/720*getWidth(), (633.3f - 2*d0)/1280*getHeight()), //bottomRight
new Point((double)60.0f/720*getWidth(), (633.3f - 3*d0)/1280*getHeight()) //botomLeft
);
4

Point detect = new Point((double)originX, (double)originY); if (left1.contains(test)) {
//Rotate right
if(dx > 50 && dy >
originY = e.getY(); mRenderer.rotateRightCube3("right1");
}
//Rotate left
if(dx <
originY = e.getY(); mRenderer.rotateLeftCube3("right1");
}
//Rotate Up
if(dy
originY = e.getY(); mRenderer.rotateUpCube3("front1");
}
//Rotate Down
if(dy > 50 && dx < 20 && dx >
originY = e.getY(); mRenderer.rotateDownCube3("front1");
}
}
The structure of the code base is somewhat similar to the
3. FUNCTIONALITIES
3.1. ACHIEVED
The achieved functionalities as of now are listed as follows:
•Working implementation for 2 by 2 and 3 by 3 One Cube version
–Colors
–Stroke
–Touch event
•Basic row rotation
5

•Change of view
–90± left rotation and right rotation
–180± rotation to the other side of view
•Step back, including the change of view
3.2.TO BE IMPLEMENTED
•Timer
•Global step view (indicate how many steps has been performed)
•Randomizer
•rotating animation(Or 3D view)
4. MATHEMATICAL DISCUSSION
In this section I will discuss my exploration of finding the permutations of One Cube.
As I have discussed in the midterm presentation. I started my exploration from the standard Rubik’s Cube and camp up with the formula for the total permutation(details can be found in the project webpage):
8! £38 £12! £212
12
Or:
8! £37 £12! £210
The approach to the above formula use the piece of the Rubik’s Cube as a unit. In terms of One Cube, the unit would then be each square in the cube.
Now consider any single square in the One Cube1. It is not hard to find the fact that, based on the definition of One Cube, this square can be placed in any 54 different locations within the cube by a sequence of valid movements. Similarly, all other 53 squares can also be placed in any 54 different locations by the same way.
The above discussion implies a classic permutation and combination problem. What is the total permutation if there are 54 different balls to be placed into 54 different box(each box contains exactly one ball)?
The answer to this question should be straight forward: 54!. However, the result is over counted a bit. In this answer, we are counting situations where the 9 red squares switched among
1The formal definition in Group theory is yet to be determined. The discussion is a rough idea
6

themselves. And in fact they are exactly the same case. Therefore, we should divide by 9!, the number of ways the 9 squares can be interchanged, and repeat this for each of the six colours:
54!
(9!)6
However, we are still over counting. If we can get from one configuration to another just by turning the cube, they aren’t really different, but we have counted them as different. In fact there are 24 different ways to turn the cube. If we randomly pick one of the six faces. We can get 4 different configuration by 90± rotation. And there are 6 faces in total so to sum up 24 is the result.
Consequently, the final result of the total permutations of One Cube is:
54! Æ 4.2123901 £1036 24 £(9!)6
This number also represents the number of different cubes you could get by peeling off all the visible colored facelets of the cube (9 on each of the 6 faces), scrambling them, and sticking them all back on.
5. CONCLUSION
The current implementation for One Cube is indeed a version that contains the core function- alities. The player is able to view all six faces of the cube with just a finger swipe, as well as rotating the rows and columns smoothly. The obvious future improvement in user experience would definitely be creating suitable animations for One Cube instead of colour flashing. Such work would require further commitment to advanced computer graphics and linear algebra skills.
7
6.APPENDICE
A. ONE CUBE PROJECT PAGE
B. CSC490 COURSE PAGE
http://www.dgp.toronto.edu/~karan/courses/csc490/winter_2014/
8
7. REFERENCE
REFERENCES
[1]Answer from Dr. Rick in the Math Forum, http://mathforum.org/library/drmath/view/54301.html
[2]Wikipedia, history of Rubik’s Cube, http://en.wikipedia.org/wiki/Rubik’s_Cube/
[3]StackOverflow, answer to "How to define if a determinate point is inside a region?",
http://stackoverflow.com/questions/12083093/
9